STATISTIK DESKRIPTIF

. .

Statistik deskriptif lebih berkenaan dengan pengumpulan dan peringkasan data, serta penyajian hasil peringkasan tersebut. Data-data statistik, yang bisa diperoleh hasil sensus, survei, jajak pendapat atau pengamatan lainnya umumnya masih bersifat acak, “mentah” dan tidak terorganisir dengan baik (raw data). Data-data tersebut harus diringkas dengan baik dan teratur, baik dalam bentuk tabel atau presentasi grafis yang berguna sebagai dasar dalam proses pengambilan keputusan (statistik inferensi).

Penyajian tabel dan grafis yang digunakan dalam statistik deskriptif dapat berupa:

Distribusi frekuensi
Presentasi grafis seperti histogram, Pie chart dan sebagainya.

Selain tabel dan grafik, untuk mengetahui deskripsi data diperlukan ukuran yang lebih eksak, yang biasa disebut summary statistics (ringkasan statistik).

Dua ukuran penting yang sering dipakai dalam pengambilan keputusan adalah:

Mencari central tendency (kecenderungan memusat), seperti Mean, Median, dan Modus
mencari ukuran dispersion, seperti Standar Deviasi dan Varians

Selain central tendency dan dispersion, ukuran lain yang dipakai adalah Skewness dan Kurtosis yang berfungsi untuk mengetahui kemiringan data (gradien data).

Kali ini akan dibahas menu dari SPSS yang berhubungan dengan statistik deskriptif, yaitu Summarize. Dalam menu ini terdapat beberapa submenu sebagai berikut:

Frequencies

Menu ini membahas beberapa penjabaran ukuran statistik deskriptif seperti Mean, Median, Kuartil, Persentil, Standar Deviasi dan lainnya.

Descriptives

Menu ini berfungsi untuk mengetahui skor-z dari suatu distribusi data dan menguji apakah data berdistribusi normal atau tidak.

Explore

Menu ini berfungsi untuk memeriksa lebih teliti sekelompok data. Alat utama yang dibahas adalah Box-Plot dan Steam & Leaf Plot, selain beberapa uji tambahan untuk menguji apakah data berasal dari distribusi normal.

Crosstabs

Menu ini dugunakan untuk menyajaikan deskripsi data dalam bentuk tabel silang (crosstab), yang terdiri aatas baris dan kolom. Selain itu menu ini juga dilengkapi dengan analisis hubungan di antara baris dan kolom, seperti independensi diantara mereka, besar hubungannya dan lainnya.

Case Summaries

Menu ini digunakan untuk melihat lebih jauh isis statistik deskriptif yang meliputi subgrup dari sebuah kasus, seperti grup “Pria” dan grup “Wanita”, bisa dibuat subgrup “Pria Dewasa” dan “Pria Remaja”, kemudian “Wanita Dewasa” dan “Wanita Remaja”, serta dibagi lagi menjadi yang tinggal di kota dan di desa, dan seterusnya.

Menu Frequencies

Contoh penggunaan Frequencies

Misalkan kita memiliki data tentang tinggi badan 25 orang mahasiswa (dalam centimeter) yang diambil secara acak.

No	Tinggi	Gender	No	Tinggi	Gender
1	170.2	Pria	14	170.4	Wanita
2	172.5	Pria	15	168.9	Wanita
3	180.3	Pria	16	168.9	Wanita
4	172.5	Pria	17	177.5	Wanita
5	159.6	Wanita	18	174.5	Pria
6	168.5	Wanita	19	186.6	Wanita
7	168.5	Pria	20	164.8	Wanita
8	172.5	Pria	21	170.4	Pria
9	174.5	Pria	22	168.9	Pria
10	159.6	Wanita	23	164.8	Wanita
11	170.4	Wanita	24	167.2	Wanita
12	161.3	Wanita	25	167.2	Wanita
13	172.5	Pria

Yang pertama kita lakukan adalah ada memasukan data terebut ke dalam editor SPSS. Pada bagian awal kita sudah mempelajari bagaimana membuat data baru dalam SPSS.

Langkah-langkahnya adalah sebagai berikut.

Mendefinisikan variabel.Ada banyak cara untuk mendefinisikan variabel, diantaranya adalah sebagai berikut.

Karena pada contoh kita ada dua variabel (Tinggi Badan & Gender), maka kita akan definisikan 2 variabel tersebut tipenya seperti apa. Pada bagian bawah menu editor data, tekan tombol Variable View. Maka akan tampak tampilan berikut:

Kolom pertama merupakan tempat untuk mendefinisikan nama-nama variabel tersebut. Pada baris pertama-kolom pertama untuk mendefinisikan nama variabel ke-1, baris kedua-kolom pertama untuk mendefinisikan nama variabel ke-2. Kita ketikan “Tinggi” untuk variabel pertama dan “Gender” untuk variabel kedua.
Untuk deklarasi Type variabel kita gunakan “Numeric” untuk variabel Tinggi dan Gender. Nantinya untuk variabel Gender kita pilih angka “1” untuk menandai gender Pria dan “2” untuk menandai gender Wanita.
Untuk Width, biasanya standar SPSS untuk numeric adalah 8, kita biarkan saja angka 8 karena sudah mencukupi untuk keprluan kita.
Untuk Decimals, untuk variabel Tinggi, karena datanya mengandung 1 angka di belakang koma, kita pilih 1. Sedangkan untuk gender karena bilangan bulat kita pilih angka 0. Untuk itu kita perlu mengganti default yang ada pada editor yaitu 2 dengan angka 1 dan 0 tersebut.
Untuk sementara biarkan submenu-submenu yang lain seperti Values, Label, Missing dll. Seperti apa adanya. Tampilan akhir dapat dilihat seperti gambar berikut ini.

Selanjutnya kita akan memasukan data yang kita punya dengan terlebih dahulu menekan tombol Data View. Lalu ketiklah data yang ada, setelah itu simpan dengan nama Deskriptif1.

Bila Anda sudah memiliki data tersebut dalam format Word atau Excel, Anda bisa langsung meng-copy data tersebut dengan cara yang biasa Anda lakukan, yaitu “Copy-Paste”. Setelah mengcopy dari data asal, maka lalu letakan pointer di baris-1 kolom-1 SPSS kemudian klim menu Edit, dan pilih submenu Paste.

Setelah data ada, lalu kita olah, yaitu ingin menampilkan deskripsi statistik dari data tersebut yaitu mengenai Mean, Standar Deviasi, Skewness, dll. Selain itu kita ingin pula menampilkan Chart dari data yang sesuai dengan sata kuantitatif, yaitu Histogram dan Bar Chart. Langkah-langkahnya sebagai berikut:

Dari baris menu, pilih menu Analyze, lalu pilih submenu Descriptive Statistics, lalu pilih lagi sumenu Frequencies (untuk menampilkan tabel frekuensi). Lalu akan tampil gambar berikut ini.

Kolom Variables(s) harus diisi dengan jenis-jenis variabel apa yang ingin kita analisis. Karena ingin dibuat frekuensi dari variabel Tinggi, maka klik variabel Tinggi, kemudia klik tanda , maka variabel Tinggi akan berpindah ke kolom Vraible(s).

Klik pilihan Statistics, maka akan tampil di layar gambar berikut:

Pilihan Statistics meliputi berbagai ukuran untuk menggambarkan data, antara lain sebagai berikut:

PercentilesValues. Untuk keseragaman klik Quartiles dan Percentile(s). Kemudian pada kotak disamping kanan Percentiles ketik 10, lalu tekan Add. Sekali lagi ketik 90 pada kotak terdahulu, dan klik lagi tombol Add. Pengerjaan ini dimaksudkan untuk membuat nilai persentil pada 10 dan 90.
Dispersion atau penyebaran data. Untuk keseragaman, semua atau keenam jenis pengukuran Dispersion dipilih semua.
Central Tendency atau pengukuran pusat data, untuk keseragaman pilih Mean dan Median.
Distribution atau bentuk distribusi data. Untuk keseragaman, klik Skewness dan Kurtosis.

Pilihan Charts…juga diklik, maka akan tampil gambar berikut ini.

Menu Charts berkenaan dengan jenis grafik yang ingin kita pilih. Dari Chart Type, untuk keseragaman kita pilih Histogram. Lalu menu With normal curve-nya akan hidup, maka kita klik juga With normal curve. Lalu klik Continue.

Sekarang editor akan kembali ke tampilan editor Frequencies seperti awal, selanjutnya kita akan memilih menu Format.

Setelah menu Format diklik, maka akan tampil gambar berikut:

Pada submenu Order by (data output akan disusun seperti apa ?) kita seragamkan saja dengan memilih output akan disusun naik (dari data terkecil ke data terbesar). Untuk itu pilih Ascending values. Selanjutnya klik OK. Maka semua proses pengisian dan pengolahan data telah selesai, dan kita akan lihat hasilnya (outputnya) pada editor Output.

Output SPSS dan Analisisnya

Selanjutnya data yang telah kita olah tersebut akan kita lihat outputnya. Berikut ini adalah output dari Descriptive.

Frequencies

Output Bagian Pertama (Statistics)

N atau jumlah data yang valid adalah 25 buah, sedangkan data yang hilang (missing) adalah nol. Ini artinya semua data bisa diproses
Mean atau rata-rata tinggi badan adalah 170,12 cm dengan standar error adalah 1,20655 cm. Penggunaan standar error of Mean adalah untuk memeriksa besar rata-rata populasi yang diperkirakan dari sampel. Untuk itu, dengan standar error of Mean tertentu dan pada tingkat kepercayaan 95% (SPSS sebagian besar menggunakan angka ini sebagai stanadar), rata-rata populasi tinggi badan menjadi:

Rata-rata Populasi = Rata-rata ± 2 standar error of Mean

= 170,12 ± (2 x 1,20655) cm

= (170, 12 + 2.4131) sampai (170, 12 - 2.4131)

= 172,5331cm sampai 167, 7069 cm

(Angka 2 digunakan karena tingkat kepercayaan 95%)

Median atau titik tengah data jika semua data diurutkan dan dibagi 2 sama besar. Angka median 170,20 cm menunjukkan bahwa 50% tinggi badan adalah 170,20 cm ke atas, dan 50%-nya 170,20 cm ke bawah.
Standar Deviasi adalah 6,03276 cm dan variansinya adalah 36,394 cm. Penggunaan standar deviasi adalah untuk menilai dispersi rata-rata dari sampel. Untuk itu, dengan standar deviasi tertentu dan pada tingkat kepercayaan 95%, rata-rata tinggi badan menjadi:

Rata-rata tingi badan = Rata-rata ± 2 x Standar Deviasi

= 170,12 ± (2 x 6,03276) cm

= 182.18552 cm sampai 170,12 cm

Perhatikan bahwa kedua batas angka berbeda tipis dengan nilai minimum dan maksimum, ini artinya sebaran data adalah baik.

Ukuran Skewnes adalah 0,572 cm. Untuk penilaian, nilai tersebut diubah ke angka rasio. Rasio kurtosis adalah = nilai kurtosis/standar error kurtosis = 0,572/0,902 = 0,63. Sebagai pedoman, bila rasio kurtosis berada antara -2 sampai dengan +2, maka distribusi data adalah normal.
Ukuran kurtosis adalah 1,460 cm
Data minimum adalah 159,60 cm sedangkan data maksimum adalah 186,60 cm
Range data = Data maksimum – Data minimum adalah 27,00 cm
Angka Persentil:

Rata-rata tinggi badan 10% responden di bawah 160,62 cm
Rata-rata tinggi badan 25% responden di bawah 167,20 cm
Rata-rata tinggi badan 50% responden di bawah 170,20 cm
Rata-rata tinggi badan 75% responden di bawah 172,50 cm
Rata-rata tinggi badan 90% responden di bawah 178,62 cm

Output bagian kedua (Tinggi)

Output ini merupakan gambaran tinggi badan responden dalam tabel frekuensi.

Output bagian ketiga (Histogram)

Terlihat grafik data berbentuk seperti lonceng, ini artinya distribusi data adalah normal atau mendekati normal (pengujian secara statistik akan dibahas nanti)

Tabel Frekuensi untuk Gender

Karena variabel gender bukan data kuantitatif namun kategori, maka tidak perlu dilakukan dskripsi statistik seperti Mean, Median, Standar Deviasi dan sebagaianya. Untuk data kualitatif chart yang sesuai adalah pie chart.

Langkah-langkah membuat Pie Chart

Buka kembali lembar kerja Deskriptif1.sav
Dari baris menu, pilih menu Analyze, lalu pilih submenu Descriptive Statistics, lalu pilih lagi sumenu Frequencies (untuk menampilkan tabel frekuensi). Lalu akan tampil gambar berikut ini.

Kolom Variables(s) harus diisi dengan jenis-jenis variabel apa yang ingin kita analisis. Karena ingin dibuat frekuensi dari variabel Gender, maka klik variabel Gender, kemudia klik tanda , maka variabel Gender akan berpindah ke kolom Vraible(s).
Pilihan Charts…juga diklik, maka akan tampil gambar berikut ini.

Menu Charts berkenaan dengan jenis grafik yang ingin kita pilih. Dari Chart Type, untuk keseragaman kita pilih Pie Chart. Lalu klik Continue
Setelah itu menu Format diklik, maka akan tampil gambar berikut:

Pada submenu Order by (data output akan disusun seperti apa ?) kita seragamkan saja dengan memilih output akan disusun naik (dari data terkecil ke data terbesar). Untuk itu pilih Ascending values. Selanjutnya klik OK. Maka semua proses pengisian dan pengolahan data telah selesai, dan kita akan lihat hasilnya (outputnya) pada editor Output.

Output Gender

Gender

	Frequency	Percent	Valid Percent	Cumulative Percent
Valid	1	11	44.0	44.0	44.0
	2	14	56.0	56.0	100.0
	Total	25	100.0	100.0

Penggunaan Menu Descriptive

Langkah-langkah penggunaan menu Desciptive:

Buka kembali file Deskriptif1.sav
Dari baris menu, pilih menu Analyze, lalu pilih submenu Descriptive Statistics, lalu pilih lagi sumenu Descriptives (untuk menampilkan tabel frekuensi). Lalu akan tampil gambar berikut ini.

Kolom Variables(s) harus diisi dengan jenis-jenis variabel apa yang ingin kita analisis. Karena ingin dibuat frekuensi dari variabel Tinggi, maka klik variabel Tinggi, kemudia klik tanda , maka variabel Tinggi akan berpindah ke kolom Vraible(s).
Klik Options, maka akan tampak di layar

Pilihan Options meliputi berbagai ukuran untuk menggambarkan data. Terlihat default dari SPSS yang memilih Mean, Standar deviasi, maksimum, minimum sebagai acuan untuk menghitung statistik deskriptif, untuk keseragaman biarkan pilihan tersebut. Kemudian klik Continue.

Maka akan terlihat kotak pilihan Save standardized values as variables yang telah diberi tanda akan digunakan pilihan tersebut. Hal ini berarti pilihan output SPSS mengenai deskripsi data. Lalu klik OK.
Maka outputnya sebagai berikut:

Descriptive Statistics

	N	Minimum	Maximum	Mean	Std. Deviation
Tinggi	25	159.60	186.60	170.1200	6.03276
Valid N (listwise)	25

Jika dilihat pada Editor data SPSS selain variabel tinggi dan gender sekarang muncul variabel baru, yaitu zTinggi seperti berikut

Analisisnya
Output bagian Pertama

Bagian ini membahas deskripsi statistik dari variabel tinggi yang meliputi Mean dan yang lainnya.

Output bagian Kedua

Bagian ini membahas penerapan z-score atau Standard Score. Dalam output SPSS, nilai z bisa dipakai untuk secara cepat melihat nilai mana yang menyimpang cukup jauh dari rata-ratanya (outlier)

Jika suatu data berdistribusi normal, suatu nilai bisa distandardisasi dengan nilai z, yaitu:

Dimana: xi = nilai data kei;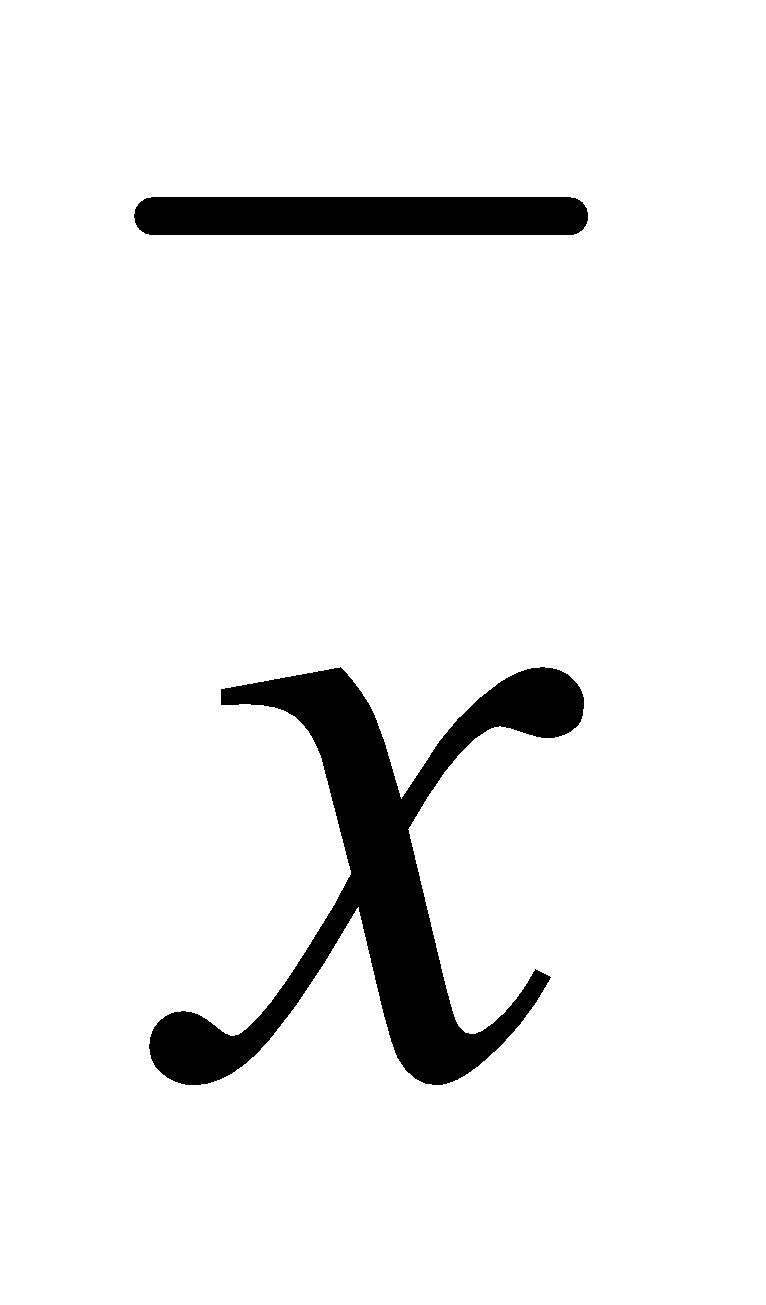

= Mean data dan s=Standar Deviasi

Sebagai contoh, lihat pada data pertama yaitu tinggi 170,20 cm, nilai z-nya dihitung dengan rumus adalah sbb:

= 0,013 (sama dengan output SPSS)

Data yang lain pun sama prinsipnya.

Melihat Data yang menyimpang (outlier)

Jika data berdistribusi normal dan tingkat kepercayaan 95%, maka tingkat signifikansi adalah 100% - 95% = 5%. Jika memakai uji dua sisi (ada tanda + dan - ), maka batas kritis ada pada 5% dibadi dua atau 2,5%. Pada tabel-z perhitungan pada satu sisi atau 50%, maka batas kritis ada pada luas kurva (50% - 2,5%) atau 47,5%.

Pada tabel-z, luas kurva untuk 47,5% didapat nilai kritis 1,96.

Dari nilai variabel zTinggi terlihat hanya ada satu data yang termasuk outlier, yaitu 186.60 cm nilai zTinggi yang di luar 1,96, yaitu zTingginya 2.73175.

Karena dari 25 data hanya ada 1 data yang outlier, maka dapat dikatakan distrubusi mendekati normal.

Analisis Crosstab (Tabel Silang)

Sebagaimana pernah dibahas di kelas bahwa salah satu analisis data kualitatif yang berskala nominal (kategori) adalah dengan Crosstab.

Analisis Crosstab untuk Uji Ketergantungan (Test of Independence)

Contoh Kasusnya:

Manajer perusahaan yang memproduksi kopi susu dalam kemasan sachet merek deCaFe ingin mengetahui bagaimana sikap konsumen terhadap produk perusahaan, serta bagaimana profil mereka.

Untuk itu 25 orang konsumen yang pernah mencicipi produk deCaFe diminta mengisi identitas dan sikap mereka terhadap produk deCaFe.

Berikut ini hasilnya:

No	Pekerjaan	Pendidikan	Gender
1	Karyawan	Akademi	Pria
2	Petani	Sarjana	Pria
3	wiraswasta	Sma	Wanita
4	Petani	Sma	Wanita
5	wiraswasta	Akademi	Wanita
6	Karyawan	Sarjana	Pria
7	wiraswasta	Sma	Wanita
8	wiraswasta	Sma	Pria
9	Petani	Akademi	Wanita
10	Petani	Akademi	Wanita
11	Karyawan	Sarjana	Pria
12	Karyawan	Sarjana	Pria
13	Petani	Sma	Wanita
14	wiraswasta	Sarjana	Pria
15	wiraswasta	Akademi	Wanita
16	Karyawan	Sarjana	Pria
17	Petani	Sma	Wanita
18	Karyawan	Akademi	Pria
19	Karyawan	Sma	Wanita
20	Petani	Akademi	Pria
21	wiraswasta	Sarjana	Wanita
22	Petani	Sarjana	Wanita
23	Petani	Sarjana	Pria
24	Karyawan	Sma	Pria
25	Karyawan	Sma	Pria

Baris pertama, menunjukkan konsumen pertama mempunyai pekerjaan karyawan dan ia seorang pria yang berpendidikan akademi. Demikian seterusnya.

Dalam SPSS otomatis no urut konsumen sudah ada, sehingga ada 3 variabel saja.

Langkah penyelesaian:

Buka lembar kerja baru
Masukkan data seperti ketika Anda memasukan data Deskriptif1.sav. Jangan lupa definsikan variabelnya. Karena semuanya data kategori pilih Decimalsnya = 0.
Untuk variabel pekerjaan, tipenya numerik, dimana: 1 = karyawan, 2= wiraswasta dan 3= petani.
Untuk variabel pendidikan, tipenya numerik dengan; 1 = Sma, 2= akademi, dan 3=sarjana
Variabel gender seperti sebelumnya, 1=Pria dan 2 = Wanita.
Setelah data diketikan lalu simpan data tersebut dengan nama file Crosstab1.sav pada drive D, dari baris menu, pilih menu Analyze, lalu pilih submenu Descriptive Statistics, lalu pilih lagi sumenu Crosstab. Lalu akan tampil gambar berikut ini.

Row(s) atau variabel yang akan ditempatkan pada baris (row) –untuk keseragaman, kita pilih Gender
Column(s) atau variabel yang akan ditempatkan pada Kolom) –untuk keseragaman, kita pilih Pekerjaan
Klik pilihan Statistics…, akan tampak dilayar gambar berikut.

Karena kita akan melihat hubungan antara dua variabel, untuk keseragaman pilih Chi-Square. Pilihan yang lainnya akan digunakan pada kasus yang relevan di bagian lain. Lalu Klik Continue
Kemudian Klik pilihan Cells…, akan tampak di layar

Pilihan Count untuk menampilkan hitungan Chi-square, apakah perlu disertakan nilai Expected (nilai yang diharapkan) selain nilai observed. Untuk keseragaman klik hanya Observed
Pilihan Percentage untuk menampilkan perhitungan angka pada baris dan kolom dalam persen. Untuk kasus ini biarkan saja kolom tersebut (tidak ada yang dipilih). Lalu klik Continue,
Klik pilihan Format…, akan tampak editor berikut

Row Order atau penempatan nama variabel dalam baris, apakah naik atau turun. Pilih Ascending. Klik Continue.
Pilihan Displayclustered bar charts dan Suppers tables biarkan kosong.

Perhatikan variabel Pendidikan tidak dimasukkan, karena dalam proses ini kita hanya memasukkan dua saja, tidak mesti semua, nanti kita akan gunakan variabel pendidikan pada kasus yang lain.
Klik OK, maka akan tampak output berikut.

Output Crosstab

Case Processing Summary

	Cases
	Valid	Missing	Total
	N	Percent	N	Percent	N	Percent
gender * Pekerjaan	25	100.0%	0	.0%	25	100.0%

Analisis Output Bagian Pertama (Case Processing Summary)

Ada 25 data yang semuanya diproses (tidak ada data missing), sehingga tingkat validitasnya 100%.

gender * kerja Crosstabulation

Count

	kerja	Total
	1	2	3
gender	1	8	2	3	13
	2	1	5	6	12
Total	9	7	9	25

Analisis Output Bagian Kedua (Crosstab antara Gender dengan Pekerjaan)

Terlihat tabel silang yang memuat hubungan diantara kedua variabel. Misalnya, pada baris-1 kolom-1, terdapat angka 8. Hal ini berarti ada 8 orang pria (variabel gender) yang mempunyai pekerjaan karyawan (varaibel Pekerjaan). Demikian pula untuk data yanag lainnya.

Chi-Square Tests

	Value	df	Asymp. Sig. (2-sided)
Pearson Chi-Square	7.702(a)	2	.021
Likelihood Ratio	8.505	2	.014
Linear-by-Linear Association	5.342	1	.021
N of Valid Cases	25

a 6 cells (100.0%) have expected count less than 5. The minimum expected count is 3.36.

Analisis Output bagian Ketiga (Uji Chi-square)

Uji Chi-square untuk mengamati ada tidaknya hubungan antara dua variabel (baris dan kolom). Di dalam SPSS, selain alat uji Chi-Square juga dilengkapi dengan beberapa alat uji yang sama tujuannya.

Hipotesis

Hipotesis untuk kasus ini:

Ho: Tidak ada hubungan antara baris dan kolom, atau antara pekerjaan konsumen dengan gender konsumen tersebut.

Hi : Ada hubungan antara baris dan kolom, atau antara pekerjaan konsumen dengan gender konsumen tersebut

Pengambilan Keputusan

Dasar pengambilan keputusan, yaitu: Berdasarkan perbandingan Chi-Quare Uji dan angka dari Tabel

Jika Chi-square Hitung < Chi-square Tabel, Maka Ho diterima
Jika Chi-square Hitung > Chi-square Tabel, Maka Ho ditolak

Chi-square Hitung dapat dilihat pada output bagian ketiga yaitu 7.702. Sedangkan Chi-square Tabel, dapat dilihat pada Tabel Uji-Statistik untuk Chi-square. Dalam hal ini untuk tingkat signifikansi () = 5% dan derajat kebebasan (dF) = 2 adalah 5,9915.

Karena Chi-square Hitung (7.702) > Chi-square Tabel (5,9915), Maka Ho ditolak Dengan demikian dipsimpulkan bahwa ada hubungan antara baris dan kolom, atau antara pekerjaan konsumen dengan gender konsumen tersebut.

Kita juga bisa menguji hipotesis dengan membandingkan nilai Probabilitas yang nilainya dapat dilihat pada bagian Asymp. Sig. (2-sided), yang dalam kasus ini sebesar 0.021. Jika nilai Probabilitas > 0,05 maka Ho diterima. Tetapi bila nilai Probabilitas < 0,05 maka Ho ditolak.

Dalam kasus ini 0.021 < 0,05 artinya Ho ditolak, atau ada hubungan antara baris dan kolom, atau antara pekerjaan konsumen dengan gender konsumen tersebut.

Dari kedua analisis tersebut bisa diambil kesimpulan yang sama, yaitu Ho ditolak atau ada hubungan antara pekerjaan seorang konsumen dengan gender konsumen tersebut. Dengan kiata lain dapat saja dikatakan bahwa kebanyakan pria berprofesi karyawan sedangkan kebanyakan wanita tidak banyak yang berprofesi karyawan, mungkin banyaknya wiraswasta.

Pada kasus dimana, Ho ditolak atau disimpulkan bahwa ada hubungan antara pekerjaan seorang konsumen dengan gender konsumen tersebut, maka dapat ditanyakan pula seberapa besar atau seberapa kuat hubungan tersebut ? Hal ini akan kita bahas pada contoh lain.

Sekarang, tugas Anda adalah berlatih untuk mencari hubungan antara variabel Pekerjaan dengan Tingkat Pendidikan, Jika sudah memasukkan datanya dalam program SPSS simpan pada drive D dengan nama Crosstab2.sav dan outputnya dengan Crosstab2out. Buatlah analisis Anda dalam file word lalu simpan pula pada drive D.

Menguji Keeratan Hubungan Dua Variabel Berskala Nominal

Jika tadi kita contohkan bahwa berdasarkan analisis Crosstab ditemukan terdapat hubungan antara dua variabel berskala nominal, yaitu antara gender dengan pekerjaan. Sekarang kita akan cari tahu seberapa besar keeratan hubungan tersebut.

SPSS menyediakan dua cara untuk mengukur hubungan tersebut, yaitu:

Symetric Measures, yaitu hubungan yang setara dan berdasarkan perhitungan Chi-square
Directional Measures, yaitu hubungan yang tidak setara dan berdasarkan pada proportional Reduction In Error (PRE)

Kedua cara perhitungan di atas dapat digunakan pada kasus hubungan antara Pekerjaan dengan Gender.

Langkah-langkahnya:

Buka lagi lembar kerja Crosstab1.sav
Darri baris menu, pilih menu Analyze, lalu pilih submenu Descriptive Statistics, lalu pilih lagi sumenu Crosstab. Lalu akan tampil gambar seperti sebelumnya.

Pada menu Row(s) atau variabel yang akan ditempatkan pada baris (row) –untuk keseragaman, kita pilih Gender
Column(s) atau variabel yang akan ditempatkan pada Kolom) –untuk keseragaman, kita pilih Pekerjaan

Klik pilihan Statistics…, akan tampak dilayar gambar berikut.

Karena sudah tahu bahwa antara kedua variabel tersebut terdapat hubungan, maka sekarang tidak perlu lagi Chi-square, oleh karena itu sekarang Chi-square-nya jangan dicentak (tidak diklik). Kalau diklik, hasilnya akan seperti terdahulu.

Klik pilihan Correlations untuk mengetahui koefisien korelasi kedua variabel dengan cara Symetric Measures.
Pada kolol Nominal (yang berarti khusus untuk data yang berskala Nomonal), klik semua pilihan yaitu Contingency Coefficient, Phi and Cramer’s V, lambda dan Uncertainty coefficient. Pilihaan ini untuk mengetahui koefisien korelasi dengan cara Directional Measures. Lalu klik Continue. Kemudian Klik pilihan Cells…, akan tampak di layar gambar sebelah kanan.

Untuk pilihan Count, ntuk keseragaman klik hanya Observed

Pilihan Percentage untuk kasus ini biarkan saja kolom tersebut (tidak ada yang dipilih). Demikian pula kolom Residuals biarkan kosong. Lalu klik Continue.

Klik pilihan Format. Row Order atau penempatan nama variabel dalam baris, apakah naik atau turun. Pilih Ascending. Klik Continue.

Pilihan Displayclustered bar charts dan Suppers tables biarkan kosong.

Selanjutnya Tekan OK untuk mendapatkan outputnya.

Output bagian Pertama

Case Processing Summary

	Cases
	Valid	Missing	Total
	N	Percent	N	Percent	N	Percent
gender * kerja	25	100.0%	0	.0%	25	100.0%

Ada 25 data yang semuanya diproses (tidak ada data missing), sehingga tingkat validitasnya 100%.

Output bagian Kedua

gender * kerja Crosstabulation

Count

	kerja	Total
	1	2	3
gender	1	8	2	3	13
	2	1	5	6	12
Total	9	7	9	25

Tabel yang menggambarkan hubungan antara variabel, misalnya pada baris-2 kolom-1 ada angka 1, artinya ada 1 orang konsumen wanita bekerka sebagai karyawan.

Output bagian Ketiga (Symmetric Measures)

Symmetric Measures

	Value	Asymp. Std. Error(a)	Approx. T(b)	Approx. Sig.
Nominal by Nominal	Phi	.555			.021
	Cramer's V	.555			.021
	Contingency Coefficient	.485			.021
Interval by Interval	Pearson's R	.472	.167	2.566	.017(c)
Ordinal by Ordinal	Spearman Correlation	.472	.173	2.566	.017(c)
N of Valid Cases	25

a Not assuming the null hypothesis.

b Using the asymptotic standard error assuming the null hypothesis.

c Based on normal approximation.

Disi

Di sini hanya diperhatikan besar korelasi antara Nominal-Nominal. Hal ini karena kedua variabel berskala nominal, karena itu besaran Pearson dan Spearman tidak relevan untuk dibahas.

Ada 3 besaran untuk menghitung korelasi antara variabel pekerjaan dengan gender, dan ketiganya mempunyai angka signifikan atau nilai Probabilitas 0,021. Karena nilai Probabilitas di bawah 5%, maka bisa dikatakan ada hubungan antara kedua variabel tersebut (seperti telah terbukti sebelumnya).

Besaran korelasi (Phi dan Cramer) menghasilkan angka sama yaitu 0,555. Sedangkan koefisien kontingensi menghasilkan angka 0,485 (lebih kecil). Dari ketiga besaran itu bisa disimpulkan adanya hubungan yang cukup erat antara (disebut erat jika mendekati angka 1 dan tidak ada hubungan bila mendekati angka 0) antara variabel pekerjaan dengan variabel jender.

Output bagian Keempat (Directional Measures)

Disini juga ada 3 ukuran untuk mengukur hubungan antara kedua variabel tersebut. Namun di sini ada pembedaan, yaitu satu variabel sebagai dependen sedangkan yang lainnya sebagai variabel independen.

Untuk lebih jelasnya lihat besaran pada korelasi lambda.

Symmetric atau kedua variabel setara (bebas), maka besar korelasinya adalah 0,393 atau cukup lemah (kurang dari 0,50). Angka signifikansinya adalah 0,045 atau di bawah 0,05 yang berarti kedua variabel memang berhubungan secara nyata.
Jika ada perkataan Dependent, dipakai pedoman (berlaku untuk ketiga alat uji) berikut:

Jika angka korelasi 0, maka pengetahuan akan variabel independen tidak menolong dalam usaha memprediksi variabel dependen
Jika angka korelasi = 1, maka pengetahuan akan variabel independen menolong dalam usaha memprediksi variabel dependen

Contoh analisis pada Lambda

Gender Konsumen Dependen atau Gender sebagai variabel dependen (tergantung), dimana Pekerjaan adalah variabel independennya. Karena angka signifikansi 0,116 lebih besar daripada 0,05 (5%), maka variabel Independen/bebas yaitu Pekerjaan tidak dapat memprediksi variabel dependen yaitu Gender.
Pekerjaan Konsumen Dependen atau Pekerjaan sebagai variabel dependen (tergantung), dimana gender adalah variabel independennya. Karena angka signifikansi 0,041 lebih besar daripada 0,05 (5%), maka variabel Independen/bebas yaitu Pekerjaan dapat memprediksi variabel dependen yaitu Gender. Tetapi Angka Korelasi lambdanya 0,313 < 0,50 ini artinya korelasinya lemah. Bisa dikatakan bahwa pengetahuan akan gender seorang konsumen tidak begitu menolong dalam mupaya memprediksi pekerjaan konsumen tersebut. Atau pekerjaan konseumen sebagai karyawan atau petani atau wiraswasta tidak bisa diperkirakan begitu saja karena ia seoraang pria atau wanita.

Analisis pada Korelasi Goodman dan Kruskal Tau

Dari angka signifikansi keduanya adalah signifikan (berbeda dengan Lambda), namun besar korelasinya juga tidak kuat. Atau variabel gender tidak bisa memprediksi secara kuat variabel Pekerjaan seorang konsumen, demikian pula sebaliknya.

Analisis pada Korelasi Uncertainty Coefficient

Dari angka signifikansi ketiganya adalah signifikan, namun besar korelasinya juga tidak kuat. Atau variabel gender tidak bisa memprediksi secara kuat variabel Pekerjaan seorang konsumen, demikian pula sebaliknya.

Analisis pada Korelasi Asymptotic Standard Error

Di sini syaratnya harus didapatkan korelasi yang signifikan. Sebagai contoh angka korelasi lambda sebesarr 0,313 yang signifikan, didapat standar error 0,137.

Pada tingkat kepercayaan 95% atau ada dua standar deviasi, maka rentang korelasi adalah: 0,313 ± (2 x 0,137) atau antara 0,039 sampai 0,587

0 Response to "STATISTIK DESKRIPTIF"